2025.08.26
機械学習×流体力学が示すエンジニアリングの未来#3
本検証では、以下の2種類の方法でサロゲートモデルの精度を評価しました。
- 初期形状に対する誤差
初期の形状に対してCFD解析を行い、その結果とサロゲートモデルの予測結果との誤差を算出しました。
- 交叉検証による誤差
交叉検証は統計学の手法の一つで、データを訓練データとテストデータに分割し、すべてのデータが少なくとも一度はテストデータとして利用されるまで繰り返す方法です。本検証では、各テストデータに対するCFD結果と予測結果の誤差を平均した値を交叉検証誤差としました。
その結果を以下の表に示します。
| サロゲートモデル | 初期形状での誤差(%) | 交叉検証での誤差(%) |
|---|---|---|
| Gaussian Process | 2.8 | 5.6 |
| Radial Basis Function | 3.1 | 11.8 |
| Gaussian Process+RBF | 0.9 | 5.7 |
この結果から、初期形状での誤差はGaussian Process+RBF併用モデルが最も高い精度を示しました。一方、交叉検証ではGaussian Process単独と併用モデルが同程度の性能を示しており、本検証ではGaussian Process+RBF併用モデルを採用しました。
サロゲートモデルを利用した遺伝的アルゴリズムによる探索の結果、得られた最適なパラメータと、そのセットアップに基づくCFD解析結果を以下に示します。
| ケース | MAIN PLATE HEIGHT (MM) |
MAIN PLATE ANGLE (度) |
FLAP ANGLE (度) |
抗力 (N) | ダウンフォース (N) | L/D |
|---|---|---|---|---|---|---|
| デフォルト | 674.3 | 2.49 | 38.7 | 763 | 2700 | 3.53 |
| 最適化 | 669 | 1.0 | 37.0 | 765 | 3450 | 4.50 |
L/D比はデフォルト比で約27%の向上が確認されました。抗力(Drag)はほぼ変わらない一方で、ダウンフォース(Downforce)が大幅に増加しており、その結果として空力効率(L/D)が向上しています。
Fig. 6. リアウィング形状の比較(黒:デフォルト、赤:最適化)
Fig.6の図からわかるように、最適化されたケースではメインプレートおよびフラップの迎角がともに小さくなり、2つのウィングの間の流路が広がっていることが確認できます。
最適化ケースでは、なぜL/D比が向上したのかを理解するため、リアウィング周囲の圧力分布と速度分布を比較しました。
Fig. 7とFig. 8にはリアウィングとその周囲の圧力分布を、Fig. 9には速度分布を示しました。
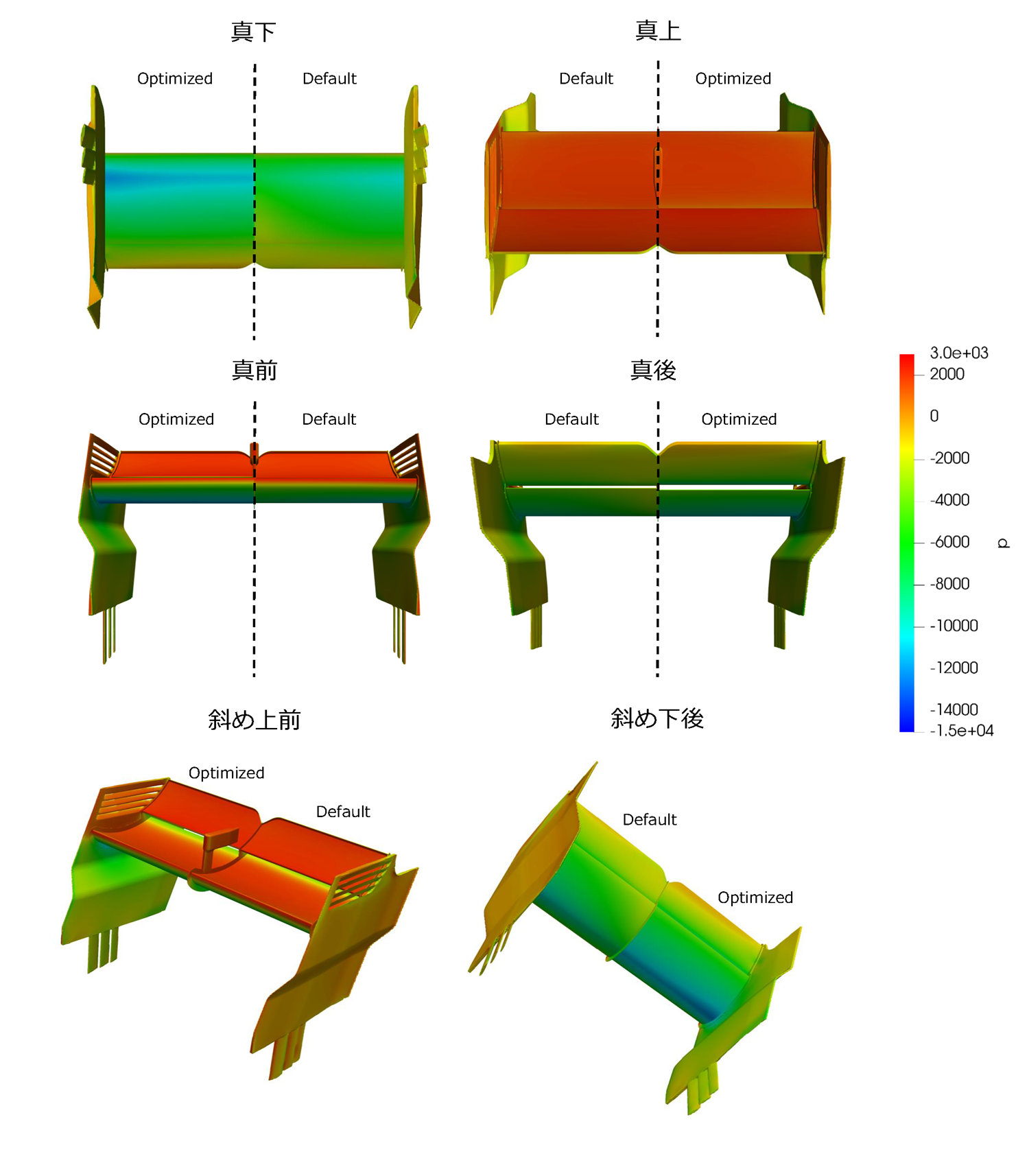
Fig. 7. リアウィングの圧力分布(左:最適化、右:デフォルト)
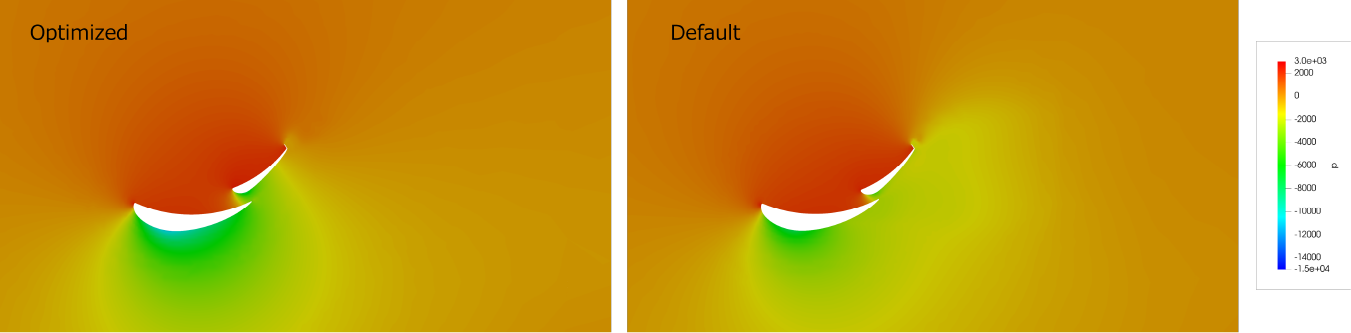
Fig. 8. 横断面における圧力分布(車軸から100 mm位置)
Fig. 9. 横断面における速度分布(車軸から100 mm位置)
メインプレート周囲の変化
まずメインプレートに注目します。
Fig. 7およびFig. 8の圧力分布を見ると、最適化ケースでは上面後端での圧力低下の開始位置が前方に移動しています。また、下面では負圧領域が広がり、さらに最低圧力も低下しています。
一方、Fig. 9の速度分布では、デフォルトケースに存在した剥離が、最適化ケースでは抑制されていることが確認できます。
この変化の要因は主に二つ考えられます。
- メインプレートの迎角を小さくしたことで、主流に対してより適切な角度となり、下面で流速が増加し圧力が低下した。
- デフォルトケースでは迎角が大きすぎて流れが剥離していたが、迎角を抑えることで剥離が防止され、速度の急激な低下を回避できた。
以上から、メインプレート下面における負圧領域の拡大と圧力の低下、剥離の抑制が、ダウンフォース増加の主因となったと考えられます。
フラップ周囲の変化
次にフラップに注目します。
Fig. 7およびFig. 8の圧力分布を比較すると、上面では両ケースに大きな差は見られません。しかし、下面では最適化ケースにおいて前縁の圧力が正から負へ大きく変化し、さらに後縁では圧力が上昇しています。
速度分布(Fig. 9)をみると、最適化ケースでは剥離の開始位置が前縁側に移動しており、メインプレートから流れてきた気流の影響が強く表れています。
この変化の要因は主に二つ考えられます。
- メインプレート迎角を小さくしたことで、上面からの流れがフラップ下面へスムーズに導かれるようになり、前縁で圧力が低下した。
- メインプレート後縁からの流れに対するフラップの角度に起因する後縁での圧力上昇は、形状と角度に起因する剥離が影響した。
ただし、前縁での強い負圧の発生が後縁での圧力上昇を上回る効果を持ち、結果的にダウンフォース増加に寄与したと考えられます。
総合的な考察
以上の解析結果から、最適化されたケースでは翼下面全体で圧力が低下し、剥離も抑制されたことが分かります。この流れ場の改善がダウンフォース増加をもたらし、最終的にL/D比の向上につながったと結論づけられます。
本検証では、サロゲートモデルと遺伝的アルゴリズムを組み合わせたデータ駆動型手法を用いて、PERRIN F1のリアウィング形状最適化を試みました。
サロゲートモデルの構築にあたっては、Gaussian Process(GP)のみを用いたモデル、Radial Basis Function(RBF)のみを用いたモデル、そしてGPとRBFを併用したモデルを比較しました。その結果、最も高いパフォーマンスを示したのはGPとRBFを併用したモデルであり、推定誤差はおよそ2〜5%に収まりました。
このサロゲートモデルを活用し、遺伝的アルゴリズムによって導かれた最適なセットアップでCFD解析を行ったところ、初期セットアップと比較してL/D比が約27%向上しました。さらに、最適化後のケースにおける圧力場と速度場の解析からは、メインプレート下面およびフラップ下面前縁において顕著な圧力低下が確認され、加えてメインプレートにおける剥離が抑制されていることが明らかになりました。これらの流れ場の改善が、ダウンフォースの増加を通じてL/D比の向上に寄与したと結論づけられます。
以上より、本検証で構築した形状最適化スキームは、一定の有効性を示しました。ただし、本検証はあくまで初期的な取り組みであり、今後の検討課題として以下の3点が挙げられます。
- パラメータ数の拡大
本検証で扱ったパラメータは限定的でしたが、F1およびAWSによるフロントウィング最適化の事例では5つのパラメータが用いられています。実際の車両開発においては、さらに多くのパラメータが必要になると考えられます。パラメータ数の増加に伴い、サロゲートモデル構築のためのデータセット拡充も必須となります。
- 推定手法の高度化
本検証ではGPとRBFを利用しましたが、より大規模なデータを扱う場合には、ニューラルネットワークをはじめとした機械学習手法の適用が有効であると考えられます。F1およびAWSの事例においても、複数の推定手法を組み合わせることで精度向上が図られていましたが、その詳細は公開されておらず、本検証では再現が困難でした。
- 学習データの改善
本検証では計算資源の制約から、RANSによるリアウィング単体での解析結果を学習データとして使用しました。しかし、より実用的なモデルを構築するためには、Detached Eddy Simulation(DES)やLarge Eddy Simulation(LES)といった非定常解析手法の導入や、フルビークル解析によるより正確なデータの利用が求められます。
以上のように、本検証は「サロゲートモデル+遺伝的アルゴリズム」による形状最適化の有効性を初期的に確認した取り組みと位置づけられます。今後、パラメータ数や推定手法、学習データの改善を進めることで、より実用的で信頼性の高い最適化スキームへと発展できると考えられます。